突然ですがクイズです。図1-1のA地点にいる牛に川の水を飲ませてから、B地点の木陰にいちばん早く連れて行くには、どういう経路をとればよいでしょうか? 正解は図1-2のように点Bを川べりの直線mに対して折り返した点B´を考え、直線AB´と直線mとの交点Cで水を飲ませればよいということになります。図1-2の経路ADB、AEBのような道のりが、それぞれADB´、AEB´の道のりに等しいことに気づけば、結局のところAからB´にいちばん早く行ける経路、すなわちAとB´を結ぶ直線を考えるのがよいと分かりますね。
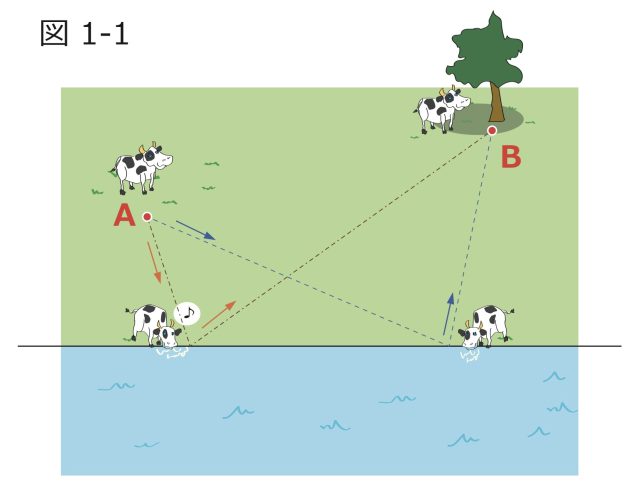
図1-1
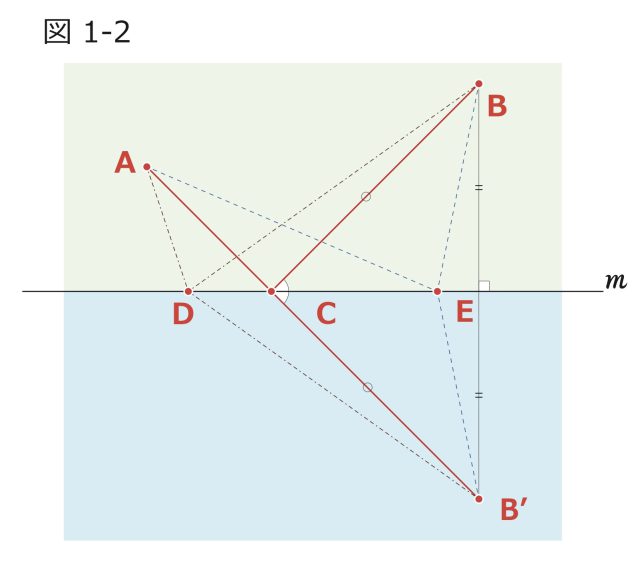
図1-2
次に、図2のように砂浜のA地点にいる人がB地点でおぼれている人を発見した場合、どういう経路で助けに行くのがいちばん早いかという問題を考えてみましょう。この場合は、真っすぐに行くことが必ずしも最短の時間で行くことにはなりません。普通、泳ぐのは走るほど速く進めないので、水上での距離を減らすために陸上で多少余分に走った方が、結局は早く着くのです。最短の時間で助けに行ける経路ACBは、助けに行く人の走る速さと泳ぐ速さとの兼ね合いによって決まります。泳ぎが苦手な人ほど、経路の折れ曲がりは大きくなります。
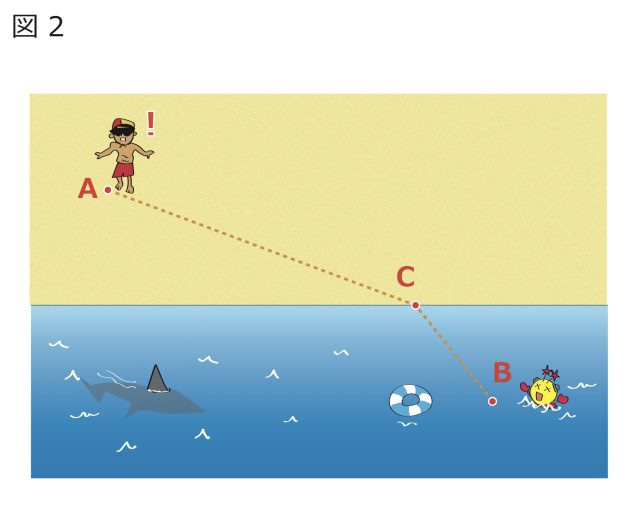
図2
ところで光が進む経路を調べてみると、驚くべきことに光は最短の時間になる経路だけを通っていることが分かります。たとえば、光が図1-2のA点から出てmのところにある鏡に反射してB点まで行くことを考えた場合、実際に光が通る経路は入射角と反射角が等しくなるようなACBだけです。また、光は空気中から水やガラス等の中に入るとき、その経路が折れ曲がる「屈折」という現象を起きます。この場合も、光が水中やガラス中を空気中のように速く進めないため、2点を最小の時間で通過しようとして折れ曲がったと解釈できます。つまり、光を大きく屈折させる物質というのは、光が速く進めない物質なのです。こんなふうに考えると、まるで光に意志があるようで面白いですね。
光が所要時間が最短になるような経路をとるということは、17世紀フランスの数学者フェルマーによって提示されました。その後、この原理は光学だけでなく、あらゆる物理学に広く応用できる原理であることが明らかになっていきます。
(文/子ども総合科学館 成島晋也)







