小学校では、「速さ」は「距離(道のり)÷時間」で計算できると習いました。例えば、家の人の車に乗って遠くまで出掛けたとき、100㎞の道のりを2時間掛けて走ったとすれば、100km÷2時間=50km/時になりますから、車は時速50kmの速さで走ったことになります。しかし、実際には2時間の間、ずっと同じ速さで走ることはありませんね。途中で加速したり、減速したり、信号で止まることもあるでしょう。ですから、この場合の時速50㎞というのは、「平均の速さ」だということになります。
ところで、車のスピードメーターは、加速したり減速したりするにつれて、その時その時の速さを表示しています。家の人もスピードメーターを見て、スピードを出し過ぎないようにしていると思います。万一、スピード違反をしたときに、「まだ1時間以上走っていないから、時速は分からないよ」とか「何時にスタートして、どのくらいの距離を走ったか分からないから、距離÷時間の割り算ができません」とか「この後はゆっくり走って、最後に距離÷時間の割り算をしたときに制限速度を超えないようにします。」などと言い訳する大人はいませんね。
このように、運転をしている大人は、「速さ」というものを、ある程度の距離を走ってから、かかった時間で割り算した量というより、その瞬間、瞬間で決まっている量として捉えているようです。この「瞬間の速さ」と距離÷時間の「平均の速さ」とはどのような関係にあるのでしょうか?
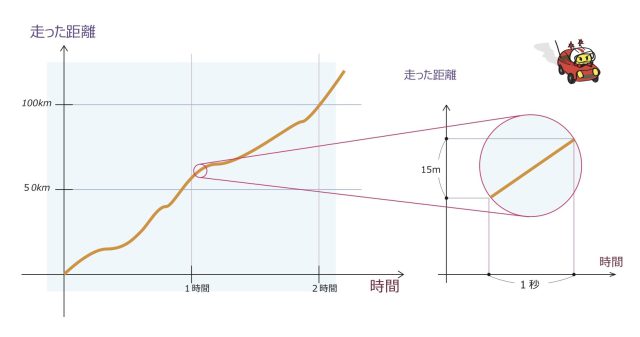
何時間というような長い時間では、車は加速したり減速したり速さが変わってしまいますが、例えば1秒間だったらほとんど同じ速さで走っていると考えられます。その間に走った距離を測ることができて、例えばそれが15mであれば、1秒はおよそ0.00028時間で15mは0.015kmなので、距離÷時間を計算すると時速は約54km/時(※)という答えになります。

更に、この1秒間に速さが変わってしまうことが心配ならば、100分の1秒や1000分の1秒、10000分の1秒というようにいくらでも短い時間に区切って同じ計算ができます。時間をどんどん短くしても、それに合わせて走る距離も短くなるので、割り算をすれば結果はそれほど変わらなくなるでしょう。「瞬間の速さ」は、距離÷時間の時間をどんどん短くしていった結果、落ち着く先の値と考えることができます。
イギリスの物理学者アイザック・ニュートンは、時間と距離の関係から瞬間の速さを導く手続きを一般化した「微分法」という計算法をつくりあげました。現在では、微分の考え方は、産業や経済等、社会の中で変化をとらえるあらゆる場面で用いられています。
(文/子ども総合科学館 成島晋也)








