理科コラム７「宇宙に果てはあるの？」では、１次元は長さの世界で、２次元が面積の世界、３次元は体積の世界という説明をしました。 では、便利道具が飛び出すドラえもんの４次元ポケットの「４次元」って何でしょう？ ヒントとして、まず数学の時間で学ぶ点の位置の表し方を図１とともに見ていきましょう。
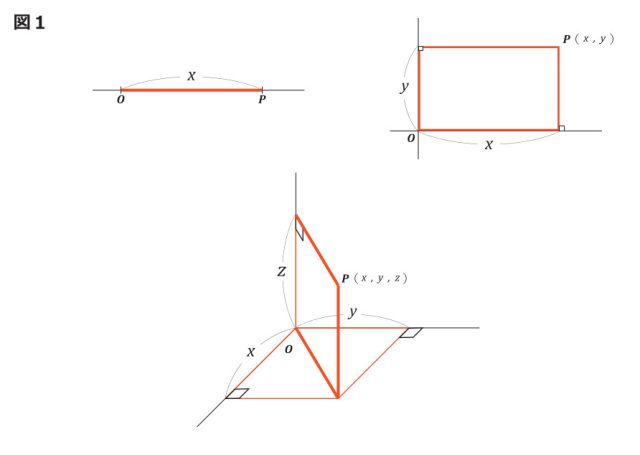
直線上の点は、原点からの距離ｘでその位置を表すことができます。ところが、平面上の点の位置は、一つの数で表すことができません。例えば、図１のような座標平面を使い、座標（ｘ,ｙ）で点の位置を表します。同様に空間の点は、三つの数の組（ｘ,ｙ,ｚ）を使って表すことができます。このように、次元は「その中の点の位置を表すのに幾つの数が必要か」と関係があります。それならば、４次元の世界は四つの数が必要だということになります。しかし、現実の世界では、縦、横、高さの三つの数字があれば全ての点の位置を表すことができてしまいます。４次元の世界の四つ目の数とは、現実と無関係の想像上の数なのでしょうか？
皆さんは、４番目の次元は時間だという話を聞いたことがあるかもしれません。確かに、いろいろな出来事を表すには場所だけでなく時間も大切なので、位置（ｘ,ｙ,ｚ）と時間ｗを一緒にして（ｘ,ｙ,ｚ,ｗ）と書けば「４つの数が必要」ということができます。そうはいっても、やはり時間と空間は別物のように感じられるので、無理やり一緒にしたようにも思えます。実は、どうしても時間と空間を一緒に考えなければならない理由があるのです。このことを、２次元の例で見ていきましょう。
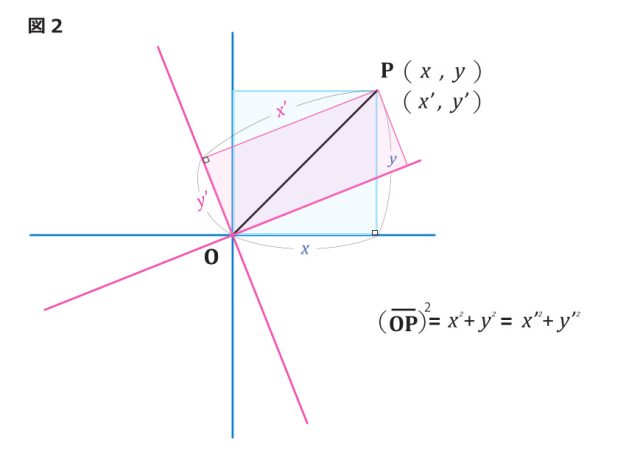
座標の基準は、自由に決めることができます。簡単にするため原点をそろえることにしても、図２のように傾いた座標平面を使ってもよいのです。そうすると、座標の値は違ってきますが、座標の値を２乗して足した数は同じになります。式で書けば、
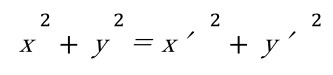
です。三平方の定理（ピタゴラスの定理）を知っている人は、この式が成り立つ理由が分かりますね。ところが、今から１００年以上も前に、時間と空間にも似たような関係
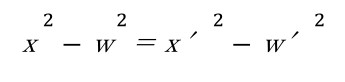（ｗは光の速さを基準にした時間）
が成り立っていることが明らかになっていました。それまでは、時間は空間と全く別物で誰にも同じように流れると考えられていたのです。この式は、時間も空間と交ざり合って、観測する人によって伸び縮みするということを意味しているのです。
ドイツの物理学者アインシュタインが１９０５年に発表した特殊相対性理論は、時間は絶対的なものではなく、３次元空間と交ざり合って４次元時空を作つくっているため、観測者によって伸び縮みすることを明らかにしました。また、１９１６年には、この４次元時空の曲がりで重力を表わす理論（一般相対性理論）を完成させました。
（文／子ども総合科学館 成島晋也）
